[T07] Esercitazione del 24 aprile 2020

Istruzioni per l’esercitazione:

• Aprite il form di consegna in un browser e loggatevi con le vostre credenziali uniroma1.
• Scaricate e decomprimete sulla scrivania il codice dell’esercitazione. Vi sarà una sotto-directory separata per ciascun esercizio di programmazione. Non modificate in alcun modo i programmi di test *_main.c.
• Rinominare la directory chiamandola cognome.nome. Sulle postazioni del laboratorio sarà /home/biar/Desktop/cognome.nome/.
• È possibile consultare appunti/libri e il materiale didattico online.
• Rispondete alle domande online sul modulo di consegna.
• Finiti gli esercizi, e non più tardi della fine della lezione:
  • zippate la directory di lavoro in cognome.nome.zip (zip -r cognome.nome.zip cognome.nome/).
• Per consegnare:
  • inserite nel form di consegna come autovalutazione il punteggio di ciascuno dei test forniti (inserite zero se l’esercizio non è stato svolto, non compila, o dà errore di esecuzione).
  • fate upload del file cognome.nome.zip.
  • importante: fate logout dal vostro account Google!
• Prima di uscire:
  • eliminate dal desktop la directory creata (rm -rf cognome.nome).
  • firmate il foglio presenze.
  • rimettete a posto eventuali sedie prese all’ingresso dell’aula!

Per maggiori informazioni fate riferimento al regolamento delle esercitazioni.

Esercizio 1 (conteggio cifre in una stringa)

Tradurre in IA32 in un file e1.s la seguente funzione, tenendo presente che i codici ASCII dei caratteri ‘0’ e ‘9’ sono 48 e 57, rispettivamente.

int count_digits(const char *s) {
    int cnt = 0;
    while (*s) {
        if (*s >= '0' && *s <= '9') cnt++;
        s++;
    }
    return cnt;
}

Usare il main di prova nella directory di lavoro E1-count-digits compilando con gcc -m32 e1_main.c e1.s -o e1.

Esercizio 2 (Palestra C)

Un tipico formato per rappresentare immagini digitali è la matrice row-major, dove le righe sono disposte consecutivamente in memoria. Per matrici a toni di grigio a 8 bit, ogni cella dell’array è compresa tra 0 (nero) e 255 (bianco). In totale, per un’immagine di altezza h e ampiezza w, l’array contiene w*h celle. La cella (0,0) è collocata nell’angolo superiore sinistro dell’immagine. Il pixel di coordinate (i,j), dove i è la coordinata verticale e j quella orizzontale, risiede nella cella di indice v[i*w+j] dell’array.

Scrivere una funzione C blur5 con il seguente prototipo:

void blur5(unsigned char* in, unsigned char* out, int w, int h){

che applica a un’immagine di input a 256 toni di grigio (unsigned char) un classico filtro che consente di sfocare l’immagine. I parametri sono:

• in: array della matrice di input da sfocare
• out: array della matrice di output sfocata
• w: ampiezza delle immagini di input e di output (indici j in [0,w])
• h: altezza delle immagini di input e di output (indici i in [0,h])

Il filtro da applicare è un semplice procedimento di convoluzione: ogni pixel di coordinate (i,j) dell’output sarà calcolato come la media aritmetica dei 25 valori in input nella finestra 5x5 centrata in (i,j). I pixel di output vicino ai bordi, la cui finestra 5x5 uscirebbe dai bordi dell’immagine di input, prendono semplicemente il valore del corrispondenti pixel di input.

Usare il main di prova nella directory di lavoro E2-blur5 compilando con gcc e2_main.c pgm.c e2.c -o e2.

Esercizio 3 (Domande)

Rispondi alle seguenti domande, tenendo conto che una risposta corretta vale 1 punti, mentre una risposta errata vale 0 punti.

Domanda 1 Dato il seguente codice in linguaggio C e la sua traduzione in linguaggio assembly, dire quale tra le seguenti tecniche di ottimizzazione è stata applicata:

• A. Constant propagation e dead code elimination
• B. Constant folding e common subexpression elimination
• C. Dead code elimination, constant folding e loop unrolling
• D. Constant folding e constant propagation
• E. Nessuna delle precedenti

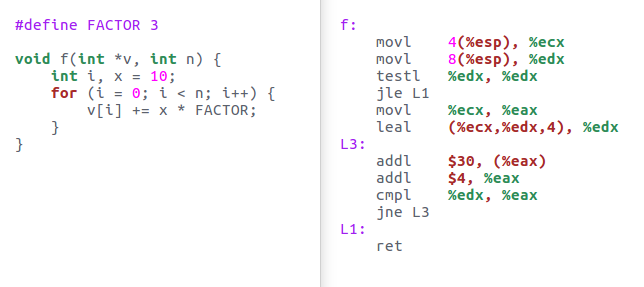
Domanda 2 Data la seguente funzione f in linguaggio C e la sua traduzione in linguaggio assembly, dire quale tra le seguenti tecniche di ottimizzazione è stata applicata:

• A. Loop unrolling
• B. Register allocation
• C. Common subexpression elimination
• D. Loop invariant code motion
• E. Nessuna delle precedenti

Domanda 3 Dato il seguente codice quale delle seguenti affermazioni risulta vera?

• A. gcc non è in grado di applicare la tecnica del loop invariant code motion in questo codice
• B. gcc è in grado di applicare la tecnica del loop invariant code motion, ma solo se g è definita nello stesso file sorgente di f
• C. gcc è in grado di applicare la tecnica del loop invariant code motion, ma solo se si attiva almeno il livello di ottimizzazione 3 (gcc -O3)
• D. gcc è in grado di applicare la tecnica del loop invariant code motion, ma solo se g viene dichiarata “static”

Domanda 4 Dato il seguente codice in linguaggio C e la sua traduzione in linguaggio assembly, dire quale tra le seguenti tecniche di ottimizzazione è stata applicata:

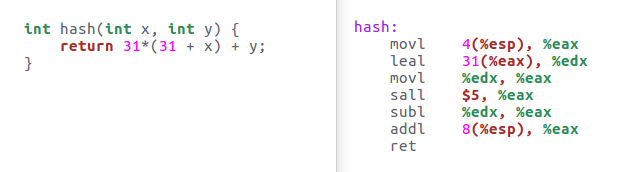
• A. Common subexpression elimination
• B. Constant propagation
• C. Constant folding
• D. Dead code elimination
• E. Strength reduction
• F. Nessuna delle precedenti

Domanda 5 Dato un programma P, supponendo di ottimizzare una porzione di codice che impegna il 40% del tempo totale di esecuzione di P, ottenendo su tale porzione di codice uno speedup di 2x, qual è lo speedup complessivo su P?

• A. circa 1.67x
• B. 1.25x
• C. 0.8x
• D. 2x
• E. Nessuna delle precedenti

Domanda 6 Dato un programma P, supponendo di ottimizzare una porzione di codice che impegna il 75% del tempo totale di P, qual è lo speedup massimo teorico che possiamo ottenere su P?

• A. Non è possibile determinare alcun limite allo speedup ottenibile su P, senza conoscere lo speedup ottenuto sulla porzione di codice ottimizzata
• B. 4/3 x
• C. 4x
• D. 0.75x
• E. Nessuna delle precedenti

Soluzioni

Esercizio 1 (Palestra IA32)

Soluzione non ancora disponibile.

Esercizio 2 (Palestra C)

e2.c

#include "e2.h"

#define IDX(i,j,w) ((i)*(w)+(j))

void blur5(unsigned char* in, unsigned char* out, int w, int h){
    int i,j,u,v;
    for (i=0; i<h; ++i)
        for (j=0; j<w; ++j)
            if (i<2 || i>h-3 || j<2 || j>w-3)
                out[IDX(i,j,w)] = in[IDX(i,j,w)];
            else {
                unsigned somma = 0;
                for (u=-2; u<=2; ++u)
                    for (v=-2; v<=2; ++v)
                        somma += in[IDX(i+u,j+v,w)];
                out[IDX(i,j,w)] = somma/25;
            }
}

Esercizio 3 (Domande)

1. D - Constant folding e constant propagation
2. E - Nessuna delle precedenti
3. A - gcc non è in grado di applicare la tecnica del loop invariant code motion in questo codice
4. F - Strength reduction
5. B - 1.25x
6. C - 4x