Collezione esercizi corso - Programmazione Funzionale e Parallela

Collezione esercizi

Sono disponibili le soluzioni per alcuni degli esercizi proposti.

Esercizio 1 (funzioni di ordine superiore)

Scrivere un metodo Scala applicaDueVolte che, dati come parametri una funzione f:Int=>Int e un intero x, calcola f(f(x)). Deve essere possibile eseguire questo programma:

val y = E1.applicaDueVolte(x=>x+1, 10)
println(y) // stampa 12

Esercizio 2 (funzioni parzialmente applicate)

Modificare il metodo applicaDueVolte dell’esercizio 1 usando la tecnica della currificazione in modo che sia parzialmente applicabile. Deve essere possibile eseguire questo programma:

val incrementaDueVolte = E1.applicaDueVolte(x=>x+1) _
val y = incrementaDueVolte(10)
println(y) // stampa 12

Esercizio 3 (funzioni su numeri - test di primalità)

Scrivere un metodo Scala che verifica se un numero è primo.

Esercizio 4 (funzioni su numeri - numeri di Fibonacci)

Scrivere un metodo Scala che calcola l’n-esimo numero di Fibonacci F(n), dove F(1)=1, F(2)=1, F(3)=2, F(4)=3, F(5)=5, ecc.

Esercizio 5 (funzioni di ordine superiore - costruzione di funzioni per casi)

Scrivere un metodo Scala concatena che, date tre funzioni f1:Double=>Double, f2:Double=>Double e f3:Double=>Double e due valori Double a e b con a<=b, restituisce una funzione che coincide con f1 per tutti gli argomenti prima di a, con f2 nell’intervallo [a,b], e con f3 dopo b.

Esercizio 6 (funzioni di ordine superiore - uguaglianza di funzioni in un intervallo)

Scrivere un metodo Scala equalInRange che, date due funzioni Int=>Int e due interi a e b, verifica se le due funzioni sono uguali nell’intervallo [a,b].

Esercizio 7 (funzioni su liste - lista occorrenze elemento in una lista)

Scrivere un metodo Scala findIndices che, data una lista generica l e un elemento x, restituisce una lista che contiene gli indici i tali che l(i)==x. Se la lista non contiene x, il metodo restituisce una lista vuota.

Esercizio 8 (funzioni su liste - verifica ordinamento)

Scrivere un metodo Scala isSorted che, data una lista di interi, verifica se è ordinata in modo non decrescente. Suggerimento: usare il metodo sliding. Elaborare sia una versione ricorsiva che non ricorsiva basata sui metodi funzionali sulle liste.

Esercizio 9 (funzioni su liste - elementi consecutivi)

Scrivere un metodo Scala consecutivi che, data una lista generica di n elementi, restituisce la lista di n-1 coppie che contiene tutti gli elementi consecutivi della lista di ingresso. Ad esempio, se in ingresso viene dato List(3,6,5,7), il metodo deve produrre List((3,6),(6,5),(5,7)). Se la lista di ingresso contiene meno di due elementi, la funzione deve produrre la lista vuota.

Esercizio 10 (funzioni su liste - rimozione duplicati)

Scrivere un metodo Scala generico removeDuplicates[T](l:List[T]):List[T] che crea una nuova lista ottenuta da l rimuovendo gli elementi duplicati.

Esercizio 11 (funzioni su liste - unione liste)

Scrivere un metodo Scala generico union[T](a:List[T], b:List[T]):List[T] che genera la lista ottenuta come unione delle liste a e b. La lista prodotta non deve contenere duplicati.

Esercizio 12 (uso di map e reduce - stringa più lunga in lista)

Scrivere un metodo Scala max che, data una lista di stringhe, restituisce la lunghezza della stringa più lunga.

Suggerimento: usare map e reduce

Esercizio 13 (funzioni su liste - funzione equal su liste, alla vaccinara)

Scrivere un metodo Scala ricorsivo equal che verifica se due liste di interi sono uguali (uguaglianza profonda).

Suggerimento: usare head, tail e isEmpty

Esercizio 14 (funzioni su liste - funzione mymap su liste, alla vaccinara)

Scrivere un metodo Scala ricorsivo mymap che, data una lista e una funzione, si comporta come la map predefinita delle liste. Esempio di uso:

val l = List(3,1,2,4,5)
println(mymap(l, _+1)) // stampa 4,2,3,5,6

Esercizio 15 (funzioni su liste - minimo e massimo di una lista)

Scrivere un metodo Scala ricorsivo minMax che, data una lista non vuota di interi, restituisce una coppia (min,max), dove min e max sono il minimo e il massimo elemento della lista, rispettivamente. Nota: data una coppia t=(a,b), t._1 è il primo elemento, t._2 è il secondo elemento.

Scrivere inoltre una variante non ricorsiva basata sui metodi standard della classe List visti a lezione.

Esercizio 16 (processamento dati di un sensore)

Un sensore misura il numero di veicoli che passano in un tratto stradale in ogni minuto, producendo una lista di interi. Occasionalmente, il sensore smette di funzionare e richiede manutenzione. Quando il sensore smette di funzionare, produce un intero negativo e da quel momento in poi i numeri prodotti sono inattendibili.

Scrivere un metodo Scala mediaVeicoli(l:List[Int]):Double che calcola il numero medio di veicoli al minuto, ignorando tutti i valori a partire dal primo negativo. Il metodo deve essere realizzato in uno stile funzionale utilizzando i metodi di ordine superiore delle liste (e non iterazione o ricorsione).

Suggerimento: usare il metodo span delle liste come documentato in http://www.scala-lang.org/api/current/#scala.collection.immutable.List. Per il cast a double, usare il metodo toDouble.

Esercizio 17 (calcolo della radice quadrata approssimata)

Un semplice algoritmo iterativo basato sul metodo di Newton per calcolare la radice quadrata di un numero x consiste nel partire da una stima iniziale y (es. y=1) e raffinarla successivamente calcolando la media tra y e x/y. Il procedimento termina quando il quadrato della stima è sufficientemente vicino a x(es. inferiore a 0.01). Completare la seguente definizione Scala usando un approccio ricorsivo:

def sqrt(x:Double) = {
   // completare...
}
println("Radice quadrata di 2 ~ "+sqrt(2))

Suggerimento: scomporre sempre un problema in funzioni più semplici. Questo non peggiora in pratica le prestazioni poiché il compilatore effettua inlining automaticamente, ma migliora molto la leggibilità, l’analisi di correttezza e la manutenibilità del codice. Definire funzioni annidate (es. per il calcolo del valore assoluto, ecc.).

Esercizio 18 (funzioni su liste - filtro su liste per indice)

Scrivere un metodo Scala filterByIndex (ricorsivo o meno) che, data una lista generica e un predicato su indici, restituisce la sottolista ottenuta prendendo solo gli elementi il cui indice soddisfa il predicato dato.

Esempio di uso:

filterByIndex(List("zero", "uno", "due", "tre"), i=>i%2==0) // prende solo gli elementi di indice pari

Esercizio 19 (funzioni su liste - data analytics)

Scrivere un metodo Scala query(studenti:List[(String,Int)], esami:List[(String,String)]):Int che, data una lista studenti di coppie (studente, età) e una lista esami di coppie (studente, esame), restituisce l’età degli studenti che hanno svolto il maggior numero di esami.

Ad esempio, se:

studenti = List(("Paola", 21), ("Luca", 22), ("Lucia", 21), ("Matteo",22))
esami = List(("Paola","PFP"), ("Luca","SC"), ("Paola","DB"), ("Lucia","LTW"), ("Matteo","SO"), ("Lucia","PFP"))

il risultato deve essere 21, infatti Paola e Lucia, che hanno 21 anni, hanno svolto complessivamente 4 esami, mentre Luca e Matteo, che hanno 22 anni, ne hanno svolti 2.

Suggerimento: usare metodi sulle liste (map, distinct, etc.)

Esercizio 20 - LSList (funzioni di ordine superiore su liste - sottosequenza più lunga)

Scrivere un metodo Scala longestSublist[T](p:T=>Boolean)(l:List[T]) che, dato un predicato p e una lista l, restituisce la più lunga sottolista di elementi consecutivi di l che soddisfano il predicato p. Se la soluzione non è unica, restituirne una qualsiasi. Ad esempio, longestSublist((_:Int)>0)(List(-4,5,3,6,0,3,4,-1)) deve restituire List(5,3,6), che è la sottolista di elementi consecutivi positivi più lunga.

Suggerimento: usare il metodo foldLeft, consultando la documentazione della classe List.

Esercizio 21 (funzioni di ordine superiore su liste - generatore di sequenze numeriche)

Scrivere un metodo Scala generateSeq che, dato un intero non-negativo n, un seme iniziale intero x e una funzione f:Int=>Int, restituisce la lista l di n interi tale che l(0)=x e l(i+1)=f(l(i)). Ad esempio, generateSeq(5, 1, _*2) restituisce List(1,2,4,8,16).

Esercizio 22 (funzioni su liste - data analytics)

Scrivere un metodo Scala query(studenti:List[(String,Int)], esami:List[(String,String)], e:Int):String che, data una lista studenti di coppie (studente, età), una lista esami di coppie (studente, esame) e un’età e, restituisce il nome dell’esame svolto dal maggior numero di studenti di età non superiore a e.

Ad esempio, se:

studenti = List(("Paola", 19), ("Luca", 23), ("Lucia", 21), ("Matteo",22), ("Francesca",23))
esami = List(("Paola","PFP"), ("Luca","SC"), ("Paola","DB"), ("Lucia","SC"), ("Matteo","LTW"), ("Lucia","PFP"), ("Francesca","SC"))
e = 22

il risultato deve essere "PFP". Infatti Paola, Lucia e Matteo, che hanno non più di 22 anni, hanno svolto complessivamente: PFP 2 volte, DB 1 volta, LTW 1 volta, e SC 1 volta.

Esercizio 23 (estensione del linguaggio con nuovi costrutti)

Il nome Scala è un acronimo di SCAlable LAnguage, che riflette il design del linguaggio orientato all’estensibilità. In Scala è possibile introdurre nuovi costrutti sfruttando il meccanismo del passaggio dei parametri per nome e la flessibilità nell’invocazione dei metodi senza dover mettere argomenti tra parentesi.

Questo esercizio richiede di definire un costrutto funzionale Scala profila { E } che valuta l’espressione E e restituisce una coppia (v,t) dove v è il valore ottenuto dalla valutazione di E e t è il tempo in nanosecondi richiesto dalla valutazione di E. Usare il seguente programma di prova:

import E23._

object E23Main extends App {
    val (v,t) = profila {
        println("Valutazione espressione...")
        (1 to 1000000).map(_.toLong).sum
    }

    println("Valore prodotto: "+v+" (corretto: 500000500000)")
    println("Tempo richiesto: "+t*1E-9+" secondi")
}

Suggerimento: per misurare il tempo, usare System.nanoTime.

Esercizio 24 (funzioni su liste di oggetti - data analytics)

Completare il seguente frammento di programma Scala:

case class Studente(nome:String, età:Int, esami:List[String])
val q = List(
                 Studente("Marco",   23, List("PFP","SC")), 
                 Studente("Laura",   19, List("SC", "FI1", "PFP")), 
                 Studente("Stefano", 23, List("SC", "FI1")), 
                 Studente("Marco",   25, List("SC", "FI1", "FI2")), 
                 Studente("Paola",   22, List("SC", "PFP"))
            )

val query1 = // estrarre tutti gli studenti con età compresa tra 20 e 24 anni (inclusi) che hanno sostenuto l'esame di "PFP"
// stampare i dati degli studenti in query1

val query2 = // estrarre tutti gli studenti con età strettamente inferiore a 24 anni che hanno sostenuto almeno due esami
// stampare i dati degli studenti in query2

Provare diverse soluzioni usando:

for comprehension (for ... yield)
metodi delle liste

Esercizio 25 (classe per numeri razionali)

Scrivere una classe Scala Rational che rappresenta numeri razionali della forma num/den, dove num e den sono interi. Scrivere la classe in modo che sia possibile eseguire il seguente codice Scala:

object E25Main extends App {
    val r1 = Rational(2, 7)
    val r2 = Rational(8, 6)
    val r3 = Rational(4, 14)
    println(r1+r2)  // stampa 34/21
    println(r1-r2)  // stampa -22/21
    println(r1*r2)  // stampa 8/21
    println(r1/r2)  // stampa 3/14
    println(r1==r3) // stampa true
    println(r1!=r3) // stampa false
    println(r1!=r2) // stampa true
    println(r1<r2)  // stampa true
    println(r2<r1)  // stampa false
}

Suggerimento: calcolare il massimo comun divisore di numeratore e denominatore per riportare la frazione ai minimi termini (o irriducibile). Ad esempio, 4/14 dovrebbe essere memorizzato in un oggetto Rational come 2/7.

Esercizio 26 (disegno di una griglia n x n - grafica 2D)

Completare il metodo Scala getGrid dell’object Model2D seguente in modo che costruisca un modello 2D che raffigura una griglia n x n. La figura è creata utilizzando esclusivamente segmenti di linea. La figura deve essere confinata nello spazio quadrato bidimensionale di lato unitario delimitato dall’origine degli assi fino al punto di coordinate (1,1). La figura viene poi scalata automaticamente dal modulo di visualizzazione per occupare la dimensione della finestra. Si ricordi che da Scala è possibile accedere a tutte le funzioni delle librerie Java (es. quelle della classe Math, se dovessero servire).

Per compilare da riga di comando usare: scalac Frame2D.scala Shape.scala Model2D.scala.

Model2D.scala:

import java.awt.Color

object Model2D {

  def getGrid(n:Int) = {

    val RED = new Color(0xFF0000) // in formato RGB (Red-Blue-Green) o anche Color.RED

    // completare costruzione di un modello 2D di una griglia con n linee verticali ed n linee orizzontali
    List(
        Line(0.0,0.5,1.0,0.5,RED), // linea rossa
        Line(0.5,0,0.5,1.0)        // linea colore default (nero)
    )
  }

  def main(args:Array[String]) {
    println("Displaying 20x20 grid...")
    Frame2D.display(Model2D.getGrid(20), 500, 500)
  }
}

Shape.scala:

import java.awt.Color

// classe astratta che rappresenta elementi grafici 2D
sealed abstract class Shape

// cerchio di raggio r centrato in (x,y) di colore c
case class Circle(x:Double, y:Double, r:Double, c:Color = Color.RED) extends Shape

// segmento di linea da (x1,y1) a (x2,y2) di colore c
case class Line(x1:Double, y1:Double, x2:Double, y2:Double, c:Color = Color.RED) extends Shape

// si veda https://docs.oracle.com/javase/7/docs/api/java/awt/Color.html
// per la documentazione sui colori

Frame2D.scala:

import java.awt.{EventQueue,Graphics,Graphics2D,Dimension}
import javax.swing.{WindowConstants,JFrame,JPanel}

object Frame2D {
  def display(l:List[Shape], width:Int, height:Int) {
    EventQueue.invokeLater(new Runnable() {
      override def run() {
        val ex = new Frame2D(l,width,height)
        ex.setVisible(true)
      }
    })
  }
}

class Frame2D(l:List[Shape], width:Int, height:Int) extends JFrame {
  class Surface2D extends JPanel {

    def doDrawCircle(c:Circle, g2d:Graphics2D) {
      val wc = (2*width*c.r).toInt
      val hc = (2*height*c.r).toInt
      val xc = (width*(c.x-c.r)).toInt
      val yc = (height-height*(c.y-c.r)).toInt - hc
      g2d.setColor(c.c)
      g2d.drawOval(xc, yc, wc, hc)
    }

    def doDrawLine(l:Line, g2d:Graphics2D) {
      val x1 = (width*l.x1).toInt
      val y1 = height-(height*l.y1).toInt
      val x2 = (width*l.x2).toInt
      val y2 = height-(height*l.y2).toInt
      g2d.setColor(l.c)
      g2d.drawLine(x1, y1, x2, y2)
    }

    def doDrawing(g:Graphics) {
      g match {
        case g2d:Graphics2D =>
          l foreach (_ match {
            case c:Circle => doDrawCircle(c, g2d)
            case l:Line   => doDrawLine(l, g2d)
          })
      }
    }

    override def paintComponent(g:Graphics) {
      super.paintComponent(g);
      doDrawing(g);
    }
  }

  val panel = new Surface2D()
  panel.setPreferredSize(new Dimension(width, height))
  add(panel);
  setTitle("Shapes");
  setResizable(false)
  pack();
  setLocationRelativeTo(null);
  setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
}

Esercizio 27 (disegno di un Mandala toroidale - grafica 2D)

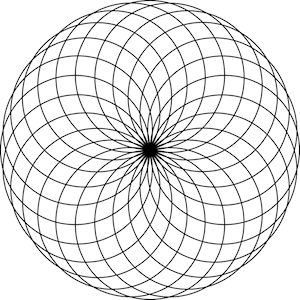
Completare il metodo getToroidalMandala dell’object ToroidalMandala seguente in modo che costruisca un modello 2D del Mandala toroidale a 24 “petali” mostrato in figura.

La figura è creata utilizzando esclusivamente cerchi. La figura deve essere confinata nello spazio quadrato bidimensionale di lato unitario delimitato dall’origine degli assi fino al punto di coordinate (1,1). La figura viene poi scalata automaticamente dal modulo di visualizzazione per occupare la dimensione della finestra. Si ricordi che da Scala è possibile accedere a tutte le funzioni delle librerie Java (es. Math.sin).

Approfondimento. I Mandala sono dei disegni di grande suggestione che rivestono un significato spirituale e rituale sia nel Buddhismo che nell’Hinduismo. Il Mandala (dal sanscrito maṇḍala (मण्डल), tradotto come “cerchio”) rappresenta, secondo i buddhisti, il processo mediante il quale il cosmo si è formato dal suo centro. Attraverso un articolato simbolismo, il Mandala consente una sorta di viaggio iniziatico che permette di crescere interiormente.

Usare il seguente programma di prova e le classi Shape e Frame2D dell’esercizio 26.

Model2D.scala:

object Model2D {

  def getToroidalMandala(numPetals:Int) = {

    // completare costruzione di un modello 2D di un Mandala toroidale
    List(Circle(0.5, 0.5, 0.5))
  }

  def main(args:Array[String]) {
    println("Displaying Toroidal Mandala...")
    Frame2D.display(Model2D.getToroidalMandala(24), 500, 500)
  }
}

Esercizio 28 (cifrario di Cesare - metodi implicit)

Il cifrario di Cesare è un antico algoritmo di cifratura che consente nel sostituire ciascuna lettera con la corrispondente lettera a una certa distanza prefissata k>=0 nell’alfabeto. Ad esempio, la cifratura a distanza k = 1 di "zorro" è "apssp". Più precisamente, la funzione di codifica a distanza k del codice ASCII c di un carattere minuscolo dell’alfabeto inglese (26 caratteri) è f(c, k) = 'a' + (c - 'a' + k) MOD 26.

L’idea viene riportata già da Svetonio in Vite dei Cesari (56, I): “Extant et ad Ciceronem, item ad familiares, id est sic structo litterarum ordine, ut nullum verbum effici posset: quae si qui investigare et persequi velit, quartam elementorum, id est D pro A et perinde reliquas commutet”.

Definire un metodo Scala def rot(k:Int):String applicabile su stringhe che applica il cifrario di Cesare a distanza k, lasciando invariati i caratteri non alfabetici. Ad esempio, "zero uno due...".rot(1) deve restituire "afsp vop evf...". Si consideri il seguente programma di prova:

import E28._

object E28Main extends App {
    def p(s:String, r:String, k:Int) = 
        println("\"" + s + "\" -> \"" + s.rot(k)  + "\" (corretto: \""+ r + "\")")
    val (s1, r1, k1) = ("Zorro", "Apssp", 1)
    val (s2, r2, k2) = ("Apssp", "Zorro", 26-1)
    val (s3, r3, k3) = ("Hello World!", "Uryyb Jbeyq!", 13)
    val (s4, r4, k4) = ("Uryyb Jbeyq!", "Hello World!", 26-13)
    p(s1, r1, k1)
    p(s2, r2, k2)
    p(s3, r3, k3)
    p(s4, r4, k4)
}

Suggerimento: usare il metodo map applicato alle stringhe, in cui è possibile “sostituire” un carattere con un altro. Le operazioni aritmetiche su caratteri lavorano sui loro codici ASCII convertiti a Int. Per riportare i codici ASCII così manipolati di nuovo a carattere si usi toChar.

Esercizio 29 (operazioni su alberi binari - classi)

Scrivere un metodo Scala sum che, dato un albero binario con elementi interi, restituisca la somma degli elementi dell’albero. Completare il seguente frammento di codice:

sealed abstract class BinTree {
    def sum = 0 // completare...
}

// albero non vuoto
case class T(l:BinTree, e:Int, r:BinTree) extends BinTree 

// albero vuoto
case class E() extends BinTree

Deve essere possibile eseguire il seguente programma di prova:

object E29Main extends App {
    val t1 = T(E(), 10, E())
    val t2 = T(E(), 5, E())
    val t3 = T(t1, 7, t2)
    val t4 = T(t3, 2, E())
    println(t1.sum + " (corretto: 10)")
    println(t2.sum + " (corretto: 5)")
    println(t3.sum + " (corretto: 22)")
    println(t4.sum + " (corretto: 24)")
}

Esercizio 30 (map su alberi binari - classi)

Scrivere un metodo Scala map su alberi binari con elementi interi che, data una funzione f:Int=>Int, restituisca un nuovo albero ottenuto da quello di partenza applicando la funzione f a ogni elemento presente nei nodi dell’albero. Completare il seguente frammento di codice:

sealed abstract class BinTree {
    def map(f:Int=>Int):BinTree = E() // completare...
}

// albero non vuoto
case class T(l:BinTree, e:Int, r:BinTree) extends BinTree 

// albero vuoto
case class E() extends BinTree

Deve essere possibile eseguire il seguente programma di prova:

object E30Main extends App {
    val t1 = T(E(), 10, E())
    val t2 = T(E(), 5, E())
    val t3 = T(t1, 7, t2)
    val t4 = T(t3, 2, E())
    val t = t4.map(_*2)
    println(t + " (corretto: T(T(T(E(),20,E()),14,T(E(),10,E())),4,E()))")
}

Esercizio 31 (elemento più frequente in una sequenza - collezioni, classe `Option`)

Si scriva un metodo Scala def piùFrequente[T](l:Seq[T]):Option[(T,Int)] che, data una sequenza di elementi generici, restituisce un Option che contiene una coppia (x,n), dove x è l’elemento più frequente ed n il suo numero di occorrenze nella sequenza, e None se la sequenza di input è vuota.

Deve essere possibile eseguire il seguente programma di prova:

object E31Main extends App {
    val s1 = Seq(1,2,4,2,1,1,5,2,4,2,5)
    val t1 = E31.piùFrequente(s1) getOrElse "errore"
    println(t1 + " (corretto: (2,4))")

    val s2 = Seq()
    val t2 = E31.piùFrequente(s2) getOrElse "errore"
    println(t2 + " (corretto: errore)")

    val s3 = Vector("uno", "due", "uno")
    val t3 = E31.piùFrequente(s3) getOrElse "errore"
    println(t3 + " (corretto: (uno,2))")
}

Suggerimento: usare i metodi groupBy e maxBy.

Esercizio 32 (intersezione veloce di liste - `Set`)

Scrivere un metodo Scala def inter[T](a:List[T], b:List[T]):List[T] che calcola l’intersezione delle liste a e b in tempo O(na+nb), dove na e nb sono le lunghezze delle rispettive liste.

Suggerimento: usare il metodo toSet per convertire liste in Set. I set forniscono il test di appartenenza alla collezione (contains) in tempo O(1) (in media) usando di default un HashSet.

Si riporta un main di prova e una versione inefficiente che usa tempo O(na*nb). Compilare il codice insieme al modulo Prof.scala che fornisce il costrutto profila per la misurazione dei tempi.

E32Main.scala:

import Prof.profila

object E32Main extends App {
    val n = 100000
    val a = List.range(1,n)
    val b = List.range(-n,5)
    println("Intersezione lenta...")
    val (v1,t1) = profila {
        E32Slow.inter(a,b)
    }
    println("Intersezione veloce...")
    val (v2,t2) = profila {
        E32.inter(a,b)
    }
    println("Tempo slow: "+t1*1E-9+" sec - Risultato: "+v1)
    println("Tempo fast: "+t2*1E-9+" sec - Risultato: "+v2)
}

object E32Slow {
    def inter[T](a:List[T], b:List[T]) = {
        val (min, max) = if (a.size < b.size) (a,b) else (b,a)
        def aux(l:List[T], res:List[T]):List[T] =
            l match {
                case Nil => res
                case h::t => if (min contains h) aux(t,h::res) else aux(t,res)
            }
        aux(max, Nil).reverse
    }
}

Prof.scala:

object Prof {
    def profila[T](body: =>T):(T,Long) = {
        val start = System.nanoTime
        val v = body
        val t = System.nanoTime - start
        (v,t)
    }
}

Esercizio 33 (sequenza infinita di numeri primi - `Stream`)

Scrivere un metodo Scala primes che genera uno stream infinito con la successione dei numeri primi: 2, 3, 5, 7, 11, ecc..

Suggerimento: scomporre il problema in sottoproblemi usando metodi ausiliari.

Usare il seguente main di prova:

E33Main.scala:

object E33Main extends App {
    val s:Stream[Int] = E33.primes
    println("Primi 5 numeri primi: "  + s.take(5) .toList)
    println("Primi 10 numeri primi: " + s.take(10).toList)
    println("Primi 20 numeri primi: " + s.take(20).toList)
}

Esercizio 34 (ricerca binaria - ordinamento naturale)

Scrivere un metodo Scala search che, dato un Vector[T] ordinato, dove sul dominio T è definito un ordinamento totale mediante la relazione <=, e un elemento e di tipo T, restituisce true se e appartiene al vettore, e false altrimenti. Il tempo di esecuzione deve essere O(log n), dove n è la lunghezza del vettore.

Suggerimento: usare l’algoritmo di ricerca binaria.

Usare il seguente main di prova:

object E34Main extends App {
    val v1 = Vector(1,3,5,6,8,9)
    val v2 = Vector()

    val r1:Boolean = E34.search(v1,8)
    val c1 = true
    println(r1 + " (corretto: " + c1 + ")")

    val r2 = E34.search(v1,0)
    val c2 = false
    println(r2 + " (corretto: " + c2 + ")")

    val r3 = E34.search(v1,100)
    val c3 = false
    println(r3 + " (corretto: " + c3 + ")")

    val r4 = E34.search(v1,1)
    val c4 = true
    println(r4 + " (corretto: " + c4 + ")")

    val r5 = E34.search(v2,1)
    val c5 = false
    println(r5 + " (corretto: " + c5 + ")")
}

Esercizio 35 - `MyRed` (replica metodo reduce - ricorsione su liste)

Scrivere un metodo Scala myReduce applicabile a liste generiche che replica il funzionamento del metodo reduce, restituendo però un Option che vale None se la lista e vuota, e Some(x) altrimenti, dove x è il risultato della riduzione. L’implementazione deve essere ricorsiva e non deve usare il metodo predefinito reduce o similari (fold ecc.), né costrutti della programmazione imperativa (var, while, ecc.).

Usare il seguente main di prova:

MyRedMain.scala:

import MyRed._

object MyRedMain extends App {
    val l = List.range(1,1000000)

    val v1 = l.myReduce(_+_)
    println("Test 1: "+v1+" (corretto: " + Some(l.reduce(_+_)) + ")")

    val v2 = List(1).myReduce(_+_)
    println("Test 2: "+v2+" (corretto: " + Some(List(1).reduce(_+_)) + ")")

    val v3 = List[Int]().myReduce(_+_)
    println("Test 3 "+v3+" (corretto: " + None + ")")
}

Esercizio 36 - `PCoin` (numero di resti possibili - parallelismo su liste)

Il metodo fornito def countChange(amount:Int, coins:List[Int]):Int calcola ricorsivamente il numero di modi in cui è possibile dare il resto per un ammontare amount usando il portafogli di monete coins. Si richiede di scrivere una versione parallela def countChangePar(amount:Int, coins:List[Int], maxThreads:Int):Int che prende come parametro aggiuntivo il numero massimo di thread che possono essere utilizzati per risolvere il problema.

PCoin.scala:

object PCoin {
    // versione sequenziale (inefficiente, nel caso peggiore richiede 2^n chiamate ricorsive, con n=coins.size) 
    def countChange(amount:Int, coins:List[Int]):Int =
        if (amount == 0) 1
        else if (coins.isEmpty || amount < 0) 0
        else countChange(amount - coins.head, coins.tail) + countChange(amount, coins.tail)

    // versione parallela, da completare
    def countChangePar(amount:Int, coins:List[Int], maxThreads:Int = Runtime.getRuntime().availableProcessors()):Int = ???
}

Si noti che Runtime.getRuntime().availableProcessors() fornisce il numero di core (logici) disponibili ed è usato come valore di default per il numero massimo di thread creati per risolvere il problema.

Suggerimento: usare il costrutto fornito Par.par per valutare in parallelo due espressioni.

Usare il seguente programma di prova e i relativi moduli richiesti:

PCoinMain.scala:

object PCoinMain extends App {
    val coins = List(10,100,1,2,5,20,10,50,1,200,100,5,20,10,10,5,1,20,50,1,5,200,2,50,20,1,1,2,5,200,100)
    val a1 = 899
    println("Versione sequenziale...")
    val (v1, t1)   = Prof.profila { PCoin.countChange    (a1, coins) }
    println("Versione parallela...")
    val (vp1, tp1) = Prof.profila { PCoin.countChangePar (a1, coins) }
    println("Test: " + vp1 + " (corretto: " + v1 + " - tempo seq: "+t1*1E-9+" sec - tempo par: "+tp1*1E-9+" sec)")
}

Par.scala

object Par {
    def par[A,B](a: =>A)(b: =>B):(A,B) = {
        var resA:Option[A] = None
        val r = new Runnable {
            def run() = resA = Some(a)
        }
        val t = new Thread(r)
        t.start()
        val resB = b
        t.join()
        (resA.get, resB)
    }
}

Prof.scala

object Prof {
    def profila[T](body: =>T):(T,Long) = {
        val start = System.nanoTime
        val v = body                        // il body passato come parametro per nome viene valutato qui
        val t = System.nanoTime - start
        (v,t)
    }
}

Esercizio 37 - `IsRot` (uguaglianza a meno di rotazioni - operazioni su sequenze)

Scrivere un metodo Scala def isRot(m:Seq[T]):Option[Int] applicabile su un oggetto l di tipo Seq che restituisce Some(n), se m è ottenibile ruotando l di n posizioni in avanti, e None altrimenti. Se vi sono più valori possibili di n, restituire il più piccolo.

Usare il seguente main di prova:

IsRotMain.scala:

import IsRot._

object IsRotMain extends App {
    val l1:Seq[Char] = "Hello world"
    val m1:Seq[Char] = "orldHello w"
    val r1:Option[Int] = l1.isRot(m1)
    val c1 = Some(4)
    println("Test 1: " + r1 + " (corretto: " + c1 + ")")

    val l2:Seq[Int] = List(0,1,2,3,4,5,6,7,8,9)
    val m2:Seq[Int] = List(3,4,5,6,7,8,9,0,1,2)
    val r2:Option[Int] = l2.isRot(m2)
    val c2 = Some(7)
    println("Test 2: " + r2 + " (corretto: " + c2 + ")")

    val l3:Seq[String] = List("one", "two")
    val m3:Seq[String] = List("Two", "one")
    val r3:Option[Int] = l3.isRot(m3)
    val c3 = None
    println("Test 3: " + r3 + " (corretto: " + c3 + ")")

    val l4:Seq[Boolean] = List(true, false, false)
    val m4:Seq[Boolean] = List(true, false, false)
    val r4:Option[Int] = l4.isRot(m4)
    val c4 = Some(0)
    println("Test 4: " + r4 + " (corretto: " + c4 + ")")

    val l5:Seq[Boolean] = List(true, false, false)
    val m5:Seq[Boolean] = List(true)
    val r5:Option[Int] = l5.isRot(m5)
    val c5 = None
    println("Test 5: " + r5 + " (corretto: " + c5 + ")")

    val l6:Seq[Short] = List(1,2,1,2)
    val m6:Seq[Short] = List(2,1,2,1)
    val r6:Option[Int] = l6.isRot(m6)
    val c6 = Some(1)
    println("Test 6: " + r6 + " (corretto: " + c6 + ")")
}

Esercizio 38 - `PIsRot` (uguaglianza a meno di rotazioni - parallelismo su sequenze)

Scrivere una versione parallela isRotPar del metodo isRot dell’esercizio IsRot usando il metodo par dell’esercizio PCoin. Si parta dalla soluzione proposta per l’esercizio IsRot.

Usare il seguente programma di prova che richiede il modulo Prof.scala dell’esercizio PCoin:

import IsRot._
import PIsRot._

object PIsRotMain extends App {
    val l1:Seq[Char] = "Hello world"
    val m1:Seq[Char] = "orldHello w"
    val r1:Option[Int] = l1.isRotPar(m1)
    val c1 = Some(4)
    println("Test 1: " + r1 + " (corretto: " + c1 + ")")

    val l2:Seq[Int] = List(0,1,2,3,4,5,6,7,8,9)
    val m2:Seq[Int] = List(3,4,5,6,7,8,9,0,1,2)
    val r2:Option[Int] = l2.isRotPar(m2)
    val c2 = Some(7)
    println("Test 2: " + r2 + " (corretto: " + c2 + ")")

    val l3:Seq[String] = List("one", "two")
    val m3:Seq[String] = List("Two", "one")
    val r3:Option[Int] = l3.isRotPar(m3)
    val c3 = None
    println("Test 3: " + r3 + " (corretto: " + c3 + ")")

    val l4:Seq[Boolean] = List(true, false, false)
    val m4:Seq[Boolean] = List(true, false, false)
    val r4:Option[Int] = l4.isRotPar(m4)
    val c4 = Some(0)
    println("Test 4: " + r4 + " (corretto: " + c4 + ")")

    val l5:Seq[Boolean] = List(true, false, false)
    val m5:Seq[Boolean] = List(true)
    val r5:Option[Int] = l5.isRotPar(m5)
    val c5 = None
    println("Test 5: " + r5 + " (corretto: " + c5 + ")")

    val l6:Seq[Short] = List(1,2,1,2)
    val m6:Seq[Short] = List(2,1,2,1)
    val r6:Option[Int] = l6.isRotPar(m6)
    val c6 = Some(1)
    println("Test 6: " + r6 + " (corretto: " + c6 + ")")

    val n = 20000
    val l = (0 to n).toVector
    val (a,b) = l splitAt 2*l.size/3
    val m = b ++ a
    println("Versione sequenziale...")
    val (v, t)   = Prof.profila { l.isRot(m) }
    println("Versione parallela...")
    val (vp, tp) = Prof.profila { l.isRotPar(m) }
    println("Test 7: " + vp + " (corretto: " + v + " - tempo seq: "+t*1E-9+" sec - tempo par: "+tp*1E-9+" sec)")
}

Esercizio 39 - `veq32` (uguaglianza di array di int - vettorizzazione)

Scrivere una funzione C int veq32(const int* a, int na, const int* b, int nb) che, dati due array di interi a e b di lunghezza rispettivamente na e nb, restituisce 1 se gli array sono uguali e 0 altrimenti. La funzione deve usare vettorizzazione SSE o AVX.

Suggerimento: si usino gli intrinsic _mm_cmpeq_epi32 e _mm_test_all_ones descritti nella guida Intel.

Usare il seguente pacchetto per realizzare e testare la soluzione:

veq32.c

#include "veq32.h"

// ---------------------------------------------------------------------
// veq32
// ---------------------------------------------------------------------
// versione vettorizzata

int veq32(const int* a, int na, const int* b, int nb) {
    // da completare...
    return 1;
}


// ---------------------------------------------------------------------
// veq32_seq
// ---------------------------------------------------------------------
// versione sequenziale

int veq32_seq(const int* a, int na, const int* b, int nb) {
    int i;
    if (na != nb) return 0;
    for (i=0; i<na; ++i)
        if (a[i] != b[i]) return 0;
    return 1;
}

veq32.h

#ifndef __VEQ32__
#define __VEQ32__

int veq32_seq(const int* a, int na, const int* b, int nb);
int veq32(const int* a, int na, const int* b, int nb);

#endif

veq32-main.c

#include <sys/time.h>
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

#include "veq32.h"

#define N    200003
#define M    1000


// ---------------------------------------------------------------------
// get_real_time
// ---------------------------------------------------------------------
double get_real_time() {
    struct timeval tv;
    gettimeofday(&tv, NULL);
    return tv.tv_sec+tv.tv_usec*1E-06;
}


// ---------------------------------------------------------------------
// do_test
// ---------------------------------------------------------------------
static void do_test(const int* a, int na, const int* b, int nb, int test_no, int print_time) {

    double start, tseq, tsse;
    int i, rseq = 0, rsse = 0;

    printf("\nTest #%d\n", test_no);

    // sequential
    start = get_real_time();
    for (i=0; i<M; ++i) rseq += veq32_seq(a, na, b, nb);
    tseq  = get_real_time()-start;

    // SSE
    start = get_real_time();
    for (i=0; i<M; ++i) rsse += veq32(a, na, b, nb);
    tsse  = get_real_time()-start;

    printf("- result: %d [expected: %d]\n", rsse, rseq);
    if (print_time) {
        printf("- sequential version: %.2f msec\n", tseq*1000);
        printf("- SSE version: %.2f msec\n", tsse*1000);
        printf("- speedup: %.2fx\n", tseq/(tsse==0.0 ? 1E-9 : tsse));
    }
}


// ---------------------------------------------------------------------
// main
// ---------------------------------------------------------------------
int main(int argc, char** argv) {

    int i;
    int* a = malloc(N*sizeof(int));
    int* b = malloc(N*sizeof(int));
    int* c = malloc(N*sizeof(int));
    assert(a != NULL);
    assert(b != NULL);
    assert(c != NULL);

    for (i=0; i<N; ++i)
        a[i] = b[i] = c[i] = 33 + i % 94;

    b[N-1] = 32;
    c[N-20] = 32;

    do_test(a, N-1, b, N-1, 1, 1);         // 1
    do_test(a, N, c, N, 2, 1);             // 0
    do_test(a, N/2, b, N, 3, 0);           // 0
    do_test(a, N, b, N, 4, 1);             // 0
    do_test(a, 10, b, 10, 5, 0);           // 1
    do_test(a+N-10, 10, c+N-10, 10, 6, 0); // 1
    do_test(a+N-10, 10, b+N-10, 10, 6, 0); // 0

    free(a);
    free(b);
    free(c);

    return 0;
}

Makefile

CC     = gcc
CFLAGS = -O1 -Wall -g
LFLAGS = -msse4.2         # modificare se serve AVX

veq32: veq32-main.c veq32.c veq32.h
	$(CC) $(CFLAGS) veq32-main.c veq32.c -o veq32 $(LFLAGS)

.phony: clean

clean:
	rm -rf veq32 *.dSYM

Esercizio 40 - `vpal32` (verifica array palindromo - vettorizzazione)

Scrivere una funzione C int vpal32(const int* v, int n) che, dato un array di interi v di lunghezza n, restituisce 1 se è palindromo (cioè se è uguale a se stesso rovesciato) e 0 altrimenti. Ad esempio, l’array {1,2,3,2,1} è palindromo. La funzione deve usare vettorizzazione SSE o AVX.

Suggerimento: si usino gli intrinsic _mm_shuffle_epi32, _mm_cmpeq_epi32 e _mm_test_all_ones descritti nella guida Intel.

Usare il seguente pacchetto per realizzare e testare la soluzione:

vpal32.c

#include "vpal32.h"


// ---------------------------------------------------------------------
// vpal32
// ---------------------------------------------------------------------
// SSE version

int vpal32(const int* v, int n) {
    // da completare...
    return 1;
}


// ---------------------------------------------------------------------
// vpal32_seq
// ---------------------------------------------------------------------
// sequential version

int vpal32_seq(const int* v, int n) {
    int i;
    for (i=0; i<n/2; ++i)
        if (v[i] != v[n-1-i]) return 0;
    return 1;
}

vpal32.h

#ifndef __VPAL32__
#define __VPAL32__

int vpal32_seq(const int* v, int n);
int vpal32(const int* a, int v);

#endif

vpal32-main.c

#include <sys/time.h>
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

#include "vpal32.h"

#define N    200003
#define M    1000


// ---------------------------------------------------------------------
// get_real_time
// ---------------------------------------------------------------------
double get_real_time() {
    struct timeval tv;
    gettimeofday(&tv, NULL);
    return tv.tv_sec+tv.tv_usec*1E-06;
}


// ---------------------------------------------------------------------
// do_test
// ---------------------------------------------------------------------
static void do_test(const int* v, int n, int test_no, int print_time) {

    double start, tseq, tsse;
    int i, rseq = 0, rsse = 0;

    printf("\nTest #%d\n", test_no);

    // sequential
    start = get_real_time();
    for (i=0; i<M; ++i) rseq += vpal32_seq(v, n);
    tseq  = get_real_time()-start;

    // SSE
    start = get_real_time();
    for (i=0; i<M; ++i) rsse += vpal32(v, n);
    tsse  = get_real_time()-start;

    printf("- result: %d [expected: %d]\n", rsse, rseq);
    if (print_time) {
        printf("- sequential version: %.2f msec\n", tseq*1000);
        printf("- SSE version: %.2f msec\n", tsse*1000);
        printf("- speedup: %.2fx\n", tseq/(tsse==0.0 ? 1E-9 : tsse));
    }
}


// ---------------------------------------------------------------------
// main
// ---------------------------------------------------------------------
int main(int argc, char** argv) {

    int i;
    int* a = calloc(N, sizeof(int));
    int* b = calloc(N, sizeof(int));
    int* c = calloc(N, sizeof(int));
    assert(a != NULL);
    assert(b != NULL);
    assert(c != NULL);

    for (i=0; i<N/2; ++i) {
        a[i] = b[i] = c[i] = 33 + i % 94;
        a[N-1-i] = b[N-1-i] = c[N-1-i] = a[i];
    }

    b[10] = 32;
    c[N/2] = c[N/2+1] = 32;

    do_test(a, N, 1, 1);        // 1
    do_test(b, N, 2, 0);        // 0
    do_test(c, N, 3, 1);        // 0
    do_test(a+10, N-20, 4, 1);  // 1

    free(a);
    free(b);
    free(c);

    return 0;
}

Makefile

CC     = gcc
CFLAGS = -O1 -Wall -g
LFLAGS = -msse4.2

vpal32: vpal32-main.c vpal32.c vpal32.h
	$(CC) $(CFLAGS) vpal32-main.c vpal32.c -o vpal32 $(LFLAGS)

.phony: clean

clean:
	rm -rf vpal32 *.dSYM

Programmazione Funzionale e Parallela

Corso di Laurea in Ingegneria Informatica e Automatica - A.A. 2021-2022

Collezione esercizi

Esercizio 1 (funzioni di ordine superiore)

Esercizio 2 (funzioni parzialmente applicate)

Esercizio 3 (funzioni su numeri - test di primalità)

Esercizio 4 (funzioni su numeri - numeri di Fibonacci)

Esercizio 5 (funzioni di ordine superiore - costruzione di funzioni per casi)

Esercizio 6 (funzioni di ordine superiore - uguaglianza di funzioni in un intervallo)

Esercizio 7 (funzioni su liste - lista occorrenze elemento in una lista)

Esercizio 8 (funzioni su liste - verifica ordinamento)

Esercizio 9 (funzioni su liste - elementi consecutivi)

Esercizio 10 (funzioni su liste - rimozione duplicati)

Esercizio 11 (funzioni su liste - unione liste)

Esercizio 12 (uso di map e reduce - stringa più lunga in lista)

Esercizio 13 (funzioni su liste - funzione equal su liste, alla vaccinara)

Esercizio 14 (funzioni su liste - funzione mymap su liste, alla vaccinara)

Esercizio 15 (funzioni su liste - minimo e massimo di una lista)

Esercizio 16 (processamento dati di un sensore)

Esercizio 17 (calcolo della radice quadrata approssimata)

Esercizio 18 (funzioni su liste - filtro su liste per indice)

Esercizio 19 (funzioni su liste - data analytics)

Esercizio 20 - LSList (funzioni di ordine superiore su liste - sottosequenza più lunga)

Esercizio 21 (funzioni di ordine superiore su liste - generatore di sequenze numeriche)

Esercizio 22 (funzioni su liste - data analytics)

Esercizio 23 (estensione del linguaggio con nuovi costrutti)

Esercizio 24 (funzioni su liste di oggetti - data analytics)

Esercizio 25 (classe per numeri razionali)

Esercizio 26 (disegno di una griglia n x n - grafica 2D)

Esercizio 27 (disegno di un Mandala toroidale - grafica 2D)

Esercizio 28 (cifrario di Cesare - metodi implicit)

Esercizio 29 (operazioni su alberi binari - classi)

Esercizio 30 (map su alberi binari - classi)

Esercizio 31 (elemento più frequente in una sequenza - collezioni, classe Option)

Esercizio 32 (intersezione veloce di liste - Set)

Esercizio 33 (sequenza infinita di numeri primi - Stream)

Esercizio 34 (ricerca binaria - ordinamento naturale)

Esercizio 35 - MyRed (replica metodo reduce - ricorsione su liste)

Esercizio 36 - PCoin (numero di resti possibili - parallelismo su liste)

Esercizio 37 - IsRot (uguaglianza a meno di rotazioni - operazioni su sequenze)

Esercizio 38 - PIsRot (uguaglianza a meno di rotazioni - parallelismo su sequenze)

Esercizio 39 - veq32 (uguaglianza di array di int - vettorizzazione)

Esercizio 40 - vpal32 (verifica array palindromo - vettorizzazione)

Esercizio 31 (elemento più frequente in una sequenza - collezioni, classe `Option`)

Esercizio 32 (intersezione veloce di liste - `Set`)

Esercizio 33 (sequenza infinita di numeri primi - `Stream`)

Esercizio 35 - `MyRed` (replica metodo reduce - ricorsione su liste)

Esercizio 36 - `PCoin` (numero di resti possibili - parallelismo su liste)

Esercizio 37 - `IsRot` (uguaglianza a meno di rotazioni - operazioni su sequenze)

Esercizio 38 - `PIsRot` (uguaglianza a meno di rotazioni - parallelismo su sequenze)

Esercizio 39 - `veq32` (uguaglianza di array di int - vettorizzazione)

Esercizio 40 - `vpal32` (verifica array palindromo - vettorizzazione)